What is an Aspherical Lens?
An aspherical lens is any lens that has an optical surface that is not spherical and may include cylindrical, toroidal, and general freeform surfaces.
In precision optics, the term asphere generally refers to an optic in which the local radius of curvature of an optical surface changes from the center, of its optical axis, to the edge and is rotationally symmetrical about the optical axis. We will be using the above definition for this blog series. Several methods and equations describe these aspherical surfaces, with the most common equation being the conic and polynomial general asphere equation (see below) and Forbes polynomials (Qcon and Qbfs).
Below is the general asphere equation where z is the surface sag, x is the distance from the center, k is the conic constant, R is the base radius, and A# is the polynomial expansion terms.
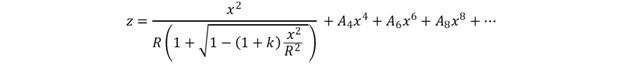
The constantly changing curvature of the aspheric surface allows the optic to correct aberrations in the optical system more efficiently than spherical lenses. As a result, this allows a more compact and lighter optical train by reducing the number of components needed and improving the overall correction of the system. Cost tends to be the trade-off for using aspheres because they are typically more expensive to manufacture than traditional spherical lenses due to the specialized knowledge and technologies required.
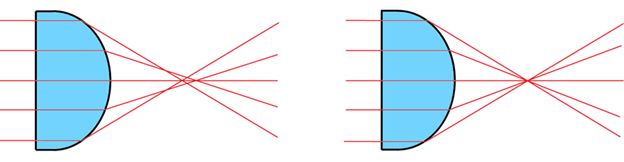
As shown in the below image, a spherical (left) and aspherical (right) lens focusing on a collimated beam of light. For the spherical surface, the light entering near the edge is focused closer to the surface than the light entering near the center. This creates a large spot size, which reduces, for example, the power density of a laser spot. The varying radius of the aspherical surface allows the lights entering the edge and center of the lens to be in focus at the same point.
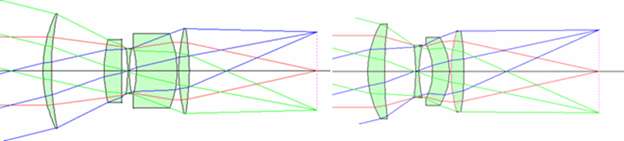
As shown below, this is a before and after image of adding an asphere in an optical system. Performance with an asphere is maintained while having fewer elements and a more compact system.
Manufacturing challenges arise from the ever-changing local radius of curvature of the aspherical surface that prevents traditional spherical tools and techniques from being used to grind, polish, and measure these surfaces. The tools used for aspheric production are single point or sub-aperture, which means they only process a small portion of the lens at any given time. As a result, this increases the processing time and allows only a single lens to be ground or polished at a time. Depending on quantities, material, and geometry, it may also be possible to mold or diamond turn an aspheric lens.
Once a designer has decided that one or more aspheric surfaces would benefit the optical system, some manufacturing and tolerancing considerations should guide the design process to ensure manufacturability and testability. These include both geometric attributes of the lens (e.g., local curvature) and design parameters (e.g., optimization diameter of the lens).
Future installations of this blog series will expand on many of the topics covered in this introduction. Check back frequently for updates!
Glossary of Asphere Related Terms
Base Radius (R): The radius used in the aspheric definition. This is the same as the vertex radius unless an A2 term is used (strongly discouraged).
Local Radius: Radius of curvature at a given location on the asphere. Unlike a spherical surface, the local radius is constantly changing on an asphere.
Vertex Radius: The local radius of curvature on the rotational axis (center) of the asphere.
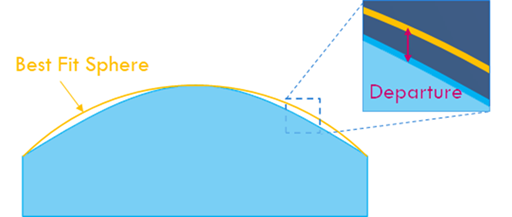
Best Fit Sphere (BFS): Most commonly refers to the radius of the sphere which intersects both the vertex and the edge of the aspheric surface over a given aperture (e.g., the edge of the optic or the clear aperture). It is aperture-dependent so it is a good practice to specify the aperture when referring to the BFS. It can also be used to refer to the spherical radius that is the closest fit to the asphere without crossing the aspheric surface. For many aspherical designs, those with only positive departure, this is the same as the sphere that intersects the center and edge. BFS may also be used to refer to the sphere which has the smallest absolute departure or volume of removal from the asphere.
Sag: Height difference, in ‘z’, from the vertex of the asphere to the point in question. The usual sign convention is for a convex surface to have positive sag, but this is not universal.
Departure: Difference between the theoretical sag of the aspheric surface and the BFS. This may be used to refer to the maximum departure on the asphere or just a specific point. The departure is measured in the ‘z’ direction, not normal to the surface.
Conic Constant (k): Defines the section of a conic to use as the base of the asphere. If k > 0 the surface is an oblate ellipse, k = 0 is spherical, -1 < k <0 is a prolate ellipse, k = -1 is parabolic, and k < -1 is hyperbolic. Occasionally, a design will specify eccentricity instead, in which case k = -e2.
Profilometer: Metrology equipment for aspheres that measures a single point at a time while scanning the surface. The most basic profilometer measurement is a single trace from one edge to the other, through the vertex. Some profilometers can do raster or spiral scans to obtain a full map of the surface error. Profilometers may contact the surface with a stylus or may use a non-contact method.
Forbes Polynomials: An alternative to the traditional asphere equation. Forbes polynomials, Qcon and Qbfs, have characteristics that aid in design for manufacturability. Not all processing and metrology tools support these equations.
Inflection Point: A point on the asphere where the local radius changes sign, e.g., from a convex to a concave radius. This may increase the difficulty of manufacturing and measuring the asphere.
Gullwing: An extreme case of an asphere with an inflection point where not only does the local radius change sign but the sag turns back on itself.





